2019. 8. 31. 01:39ㆍ통계학이론/통계학개론
안녕하세요 리그레션입니다! 이제 날씨가 조금씩 풀리려나 봅니다. 다들 몸 관리 철저하게 하고 계시죠? 감기에 지지 말고 다 같이 건강하게 공부해요~ 전 오늘 몸이 안좋아서 집에서 하루 일을 쉬고 숙면을 취했습니다. 더위먹어서 감기에 걸리긴 처음인것 같네요. 전 실패했지만 여러분들 만이라도 더위 먹지 않으시길 바랍니다. 오늘은 모비율에 관한 추론에 대해 다뤄보려고 합니다.
평균의 추정에서 사용한 이론들은 모비율의 추정 문제에도 적용할 수가 있는데요, 예를 들어 모집단 크기 500명의 사람들 중 표본을 뽑아 실업률에 관한 추론을 하고 있다고 하면요, 모집단으로부터 n개의 원소를 임의로 추출하여 표본 중 어떤 속성을 가진 것의 개수를 X라고 합니다. 이때 모비율 p의 가장 자연스러운 추정량은 표본비율 P_hat이라고 하겠습니다.

표본의 크기가 n인 모집단의 크기에 비하여 작을 때 확률변수 X는 이항분포를 따르고 평균 np, 표준편차 루트 npq가 됩니다. (q는 1-p값이죠) 그리고 앞선 포스트에서 얘기한 대로, n이 클 때는 이항 확률변수 X가 근사적으로 정규분포를 따라서 평균이 np, 표준편차가 루트 npq가 됩니다. 즉 표준 정규 분포를 따른다는 말이죠.
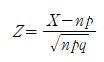
그럼 표본비율 P_hat이 모비율p의 점 추정량 임을 직관적으로 알 수 있지 않나요? 애초에 모비율을 추론하기 위해 설정한 표본비율인데, 그렇게 나와야 우리가 표본비율을 구해내는 가치가 있습니다. 확률변수 X가 이항 분포를 따른다는 가정하에, E(X)는 np, sd(X)는 루트 npq가 나오고, P_hat은 X/n이므로, 기댓값의 성질에 의하여 E(P_hat)=p / sd(P_hat)=루트{pq/n}가 됩니다.
정확히 말하자면, P_hat의 평균이 모비율p이고, P_hat의 표준편차는 루트 qp/n이 되는 거죠. 그리고 n이 클 때, 추정 오차 인 (P_hat-p)의 절댓값이 2 곱하기 (S.E. 의 추정 값) 보다 작을 확률은 약 0.954입니다.
예를 들어 쉽게 설명 드릴게요, 인터넷 판매 회사에서 새로운 품목을 시판하고자 할 때 9000명이 넘는 가입 회원 중 250명을 임의로 추출하여 견본을 발송한 결과 70명이 구입 의사가 있다고 할 때, 전체 가입 회원 중 이상품을 살 것으로 기대되는 회원의 모비율 P에 대한 점 추정 값과 95.4% 오차한계를 구하는 방법은 어떻게 될까요?
먼저 n=250, X=70으로 둔 다음, 모비율의 추정값은 70/250 은 0.28로, 이것이 P_hat이 되죠. 피하아의 표준편차의 추정 값은 루트 0.28 곱하기 0.72 나누기 250, 즉 0.028이 됩니다. 당연히 오차한계는 여기에 2를 곱한 0.056이 나오겠죠?
감사합니다. 이상 리그레션이었습니다.
'통계학이론 > 통계학개론' 카테고리의 다른 글
| 스물여덟번째 이야기 - 소표본에서의 Mu의 추론 (1) | 2019.09.04 |
|---|---|
| 스물일곱번째 이야기 - 소표본에서의 추론, t분포 유래, 소개 (0) | 2019.09.02 |
| 스물다섯번째 이야기 - 단측가설과 양측가설 (0) | 2019.08.29 |
| 스물네번째 이야기 - 모평균의 가설검정 대립가설, 귀무가설 다시 한번 정리 -2 (0) | 2019.08.28 |
| 스물세번째 이야기 - 모평균의 가설검정 대립가설, 귀무가설 다시 한번 정리 -1 (0) | 2019.08.27 |