2019. 8. 29. 01:00ㆍ통계학이론/통계학개론
안녕하세요 리그레션입니다. 오늘은 단측 가설과 양측 가설에 대해 다룰 텐데요, 많은 분들이 왜 이런 일이 일어나는지, 어떤 때 양측, 단측을 써야 하는지를 헷갈려하십니다. 언제 한쪽이 a/2 인지 a인지, 언제 이걸 정확히 적재적소에 맞게 쓰는지도요. 오늘 한번 제대로 알아볼까요?
이제까지의 포스트에서 대부분 제가 단측 가설(one-sided hypothesis)이라고 하는데, 그 이유는 대립 가설에서의 모수 Mu의 값들이 귀무가설에서 주어진 값 Mu0의 한쪽에만 놓여 있기 때문입니다. 그리고, 이 가설들의 검정을 단측 검정이라고 합니다. 그러나, 귀무가설이 Mu=Mu0이고 대립 가설은 Mu와 Mu0가 다르다인 양측 대립 가설(Two-sided alternative)의 검정을 필요로 할 때도 있습니다. 이 경우 Xbar 가 Mu0로부터 어느 쪽으로 건 멀리 떨어진 값이면, 즉, 관측값 z가 너무 작거나 너무 크면 귀무가설을 기각합니다. 유의 수준 a인 검정을 하기 위하여 기각할 확률 a를 양쪽 꼬리에 균등하게 나누어 기각역

을 정합니다. 이 기각역은 이렇게도 표현할 수 있습니다. 전 이 표현을 주로 씁니다. 짧잖습니까 후후.

표본의 크기가 클 때, Mu에 대한 가설검정은 정규 통계량(표준정규분포) Z를 검정 통계량으로 사용합니다. 대립 가설이 단측이냐 양측이냐에 따라서 기각 역도 단측 기각 역이나 양측 기각 역이냐가 결정되게 됩니다. 구체적으로 말하자면, 유의 수준 a일 때 기각역은 다음과 같습니다.
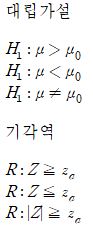
n이 클때는 중심 극한 정리가 성립하므로 모집단의 분포의 모양에 관한 아무런 가정도 필요 없습니다.
간단하게 설명드리자면, 어떤 실험에서 특정 값보다 평균이 크냐, 작냐로 나오면 단측 검정, 특정 값과 평균이 같냐 다르냐로 묻는다면 양측 검정을 하면 됩니다.
추가로 말씀드리자면, R처럼 코드를 일일이 작성하는 경우엔 패키지를 잘 모르는 경우, 이런 통계적 지식들이 확실하게 잡혀있지 않으면 안 됩니다. 하지만 SAS와 SPSS처럼 어느 정도 툴이 잡혀있는 경우엔 a를 써야 할지 a/2를 써야 할지를 자동으로 설정해 주는 경우가 많습니다.
이 포스트에서 기회를 빌어 말씀드리자면, 자동으로 써주는 프로그램이 있으면 너무나 좋겠지만, 우리는 현장에서 여러 상황들에 대처하려면 어쩔 수 없이 통계학 개론 이론부터 열심히 배우는 수밖에 없다고 생각합니다. 주변 학우들도 보면 a/2를 써야 할지 a를 써야 할지를 아직도 헷갈려하는 경우가 다반사입니다. 특이한 게 아닙니다. 왜 하는지를 정확히 알고 쓰는 것과 고등학교 수학처럼 그냥 외운 것을 줄줄 쓰는 것과는 천지차이인 것 같습니다.
감사합니다. 이상 리그레션이었습니다.
'통계학이론 > 통계학개론' 카테고리의 다른 글
| 스물일곱번째 이야기 - 소표본에서의 추론, t분포 유래, 소개 (0) | 2019.09.02 |
|---|---|
| 스물여섯번째 이야기 - 모비율에 관한 추론 (0) | 2019.08.31 |
| 스물네번째 이야기 - 모평균의 가설검정 대립가설, 귀무가설 다시 한번 정리 -2 (0) | 2019.08.28 |
| 스물세번째 이야기 - 모평균의 가설검정 대립가설, 귀무가설 다시 한번 정리 -1 (0) | 2019.08.27 |
| 스물두번째이야기 - 대표본에서의 Mu의 신뢰구간 (0) | 2019.08.26 |