2019. 8. 10. 01:00ㆍ통계학이론/통계학개론
안녕하세요 리그레션입니다. 오늘은 정규분포와 표준 정규분포에 관한 이야기를 할 건데요, 아마 역대 가장 의미 있는 포스트가 될 것 같네요 ㅠㅠ 그만큼 매우 중요한 개념이니 이해해주세요^^.
정규분포(normal distribution)는 종모양의 곡선으로 이미 잘 알려져 있습니다.
먼저 역사적으로 피에르 라플라스와 칼 가우스에 의해 발견되었고, 특히 가우스는 오차의 정규 법칙이라고 불렸던 측정오차의 확률 분포로부터 정규분포를 수리적으로 유도해내는 데에 성공했습니다. 덕분에 정규분포는 여러 학문에 걸쳐 없어서는 안 될 존재로 자리매김했죠.
하지만 부정적 측면에서는, 초기의 통계학은 한때 정규분포를 지나치게 숭배했습니다. 모든 현실은 자료가 종모양의 정규곡선을 나타내어야 한다고 믿었고, 그렇지 않으면 자료 수집 과정을 의심할 정도였습니다.
자 그럼 정규분포를 정의해 볼까요?

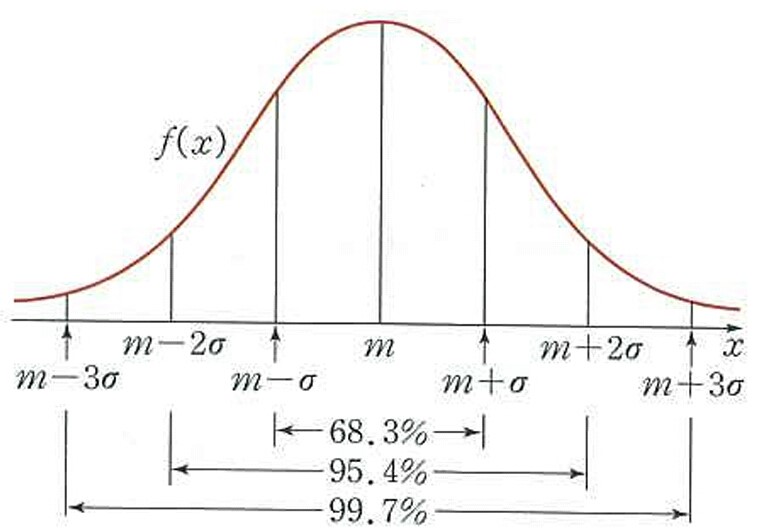
정규 분포곡선의 몇 가지 성질을 말씀드리자면

표준 정규분포는 무엇일까요? 바로 평균이 0이며 표준편차가 1인 정규분포를 우리는 표준 정규분포(standard normal distribution)라고 일컫습니다. 일반적으로 Z라고 표기합니다. N(0,1)이라는 뜻이지요.

표준정규분포는 표준 정규분포표라는 표를 따로 가지고 있습니다. 평균과 표준편차가 정해진 상황에서 확률이 같은 x값을 가지면 같게 나오기 때문에 예외가 나올 수가 없습니다.

그리고 평균인 0을 기준으로 왼쪽과 오른쪽의 확률은 0.5로 똑같습니다.
P [Z <=z]의 확률은 z의 왼쪽 곡선 아래 면적을 뜻합니다.
만약 이에 단일등호로 이루어졌을 경우엔 간단하지만 양측이 등호로 막혀있다면 어떻게 해야 할까요?
P [a=<Z <=b] 같은 경우엔, b의 왼쪽 면적에서 a의 왼쪽 면적을 빼주면 됩니다.
즉 z가 1.45일 경우, 0.9265입니다. 만약 위의 표에 있는 예시처럼 평균에서 자르고 싶다면, 0.5를 빼주면 간단하게 0.4265를 구해줄 수 있겠죠?
z=1.45 앞의 영역은 어떻게 구할까요? 바로 1에서 0.9265를 빼면 간단하게 나옵니다. 곡선 밑의 면적의 합은 1이라는 사실을 언제가 기억하시길 바랍니다.
그럼 이렇게 표준정규분포와 정규분포를 나누는 이유는 무엇일까요?
정규분포는 확률계산을 할 때 기본적으로 표준 정규분포를 이용해야 합니다. 따라서 둘은 떼려야 뗄 수가 없는 관계죠.
이 과정을 표준화라고도 합니다.

이상 정규분포와 표준정규분포에 관해 알아보았습니다. 아주 중요하니 머릿속에 쏙쏙 넣으셨으면 좋겠어요. 무더운 날씨 몸 관리 잘하시길 바랍니다. 감사합니다. 리그레션이었습니다.
'통계학이론 > 통계학개론' 카테고리의 다른 글
| 열아홉번째 이야기 - 모평균의 점추정 (0) | 2019.08.17 |
|---|---|
| 열여덟번째 이야기 - 중심극한정리 (0) | 2019.08.14 |
| 열여섯번째 이야기 - 연속 확률변수의 확률모형 (0) | 2019.08.09 |
| 열다섯번째 이야기 - 모비율의 가설검정(기각역, 검정통계량,유의수준, 귀무가설,제 1,2종 오류) (0) | 2019.08.07 |
| 열네번째 이야기 - 이항분포 (0) | 2019.08.06 |