2019. 8. 9. 01:00ㆍ통계학이론/통계학개론
안녕하세요 리그레션입니다! 오늘은 연속 확률변수의 확률 모형에 대해 알아볼 건데요~
지금까지 주로 제가 이산 확률분포의 확률변수를 다루었었죠. 이번에는 임의 값을 갖는 연속 확률변수의 분포를 설명하려고요. 연속적인 척도로 측정된 변수로 무게, 힘, 온도 등이 있습니다.
히스토그램을 직사각형이 아니라 수없이 많은 개수로 밑변을 잘랐다고 생각하시면 쉬울 것 같습니다. x의 값을 특정해서 딱딱 자연수처럼 나누지 못하고, 무게(소수 무한 대자리까지 나타낼 수 있는) 같은 것을 나타낼 때를 떠올리세요

히스토그램을 정교화하는 과정은 직사각형을 그림과 같이 곡선 형태에 근사하게 그리는 겁니다. 이 곡선을 연속 확률변수 X의 확률 밀도 곡선(probability density curve)이라고 합니다. 이 곡선의 수학적 함수 f(x)를 연속함수 확률변수 X의 확률 밀도 함수(probability density function)이라고 합니다.
확률 밀도 함수의 성질
1) 확률 밀도 곡선 아래쪽의 총면적은 1입니다.
2) P [a=<X=<b] = a와 b사이의 확률 밀도 곡선 아래쪽 면적
3) 임의의 x에 대하여 f(x) >= 0입니다.
이산 확률분포와는 다르게 P [X=x]=0입니다. 특정 점에서의 확률은 0입니다.

특정 점에서의 확률을 전혀 신경 써줄 필요가 없으므로 등호를 신경 써주시지 않으셔도 됩니다.
이산형 분포에서는 성립하지 않을 수 있으니 주의해주세요.
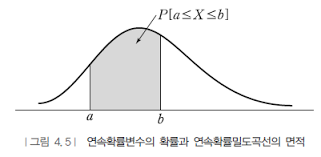
이렇게 면적을 따질 때는 P [a <X <b]=(b의 왼편 면적)-(a의 왼편 면적)으로 생각해주시면 괜찮습니다.
그리고 참고로 더 알려드리자면, 그래프가 한쪽 방향으로 긴 꼬리를 가진 형태를 비대칭적(skewed)이라고 합니다.
그리고 중앙값은 이 그래프에서 나타낼 때 곡선 아래의 면적을 정확히 반으로 나눈 X의 값이 됩니다.
이렇게 이상 연속형 확률분포에 대해 다루었는데요, 이산형을 다룰 때보다 좀 부주의(?)하게 다뤄도 된다는 메리트가 있습니다. 개인적으로 좋아합니다 ㅎㅎ. 감사합니다 리그레션이었습니다.
'통계학이론 > 통계학개론' 카테고리의 다른 글
| 열여덟번째 이야기 - 중심극한정리 (0) | 2019.08.14 |
|---|---|
| 열일곱번째 이야기 - 정규분포와 표준 정규분포 (0) | 2019.08.10 |
| 열다섯번째 이야기 - 모비율의 가설검정(기각역, 검정통계량,유의수준, 귀무가설,제 1,2종 오류) (0) | 2019.08.07 |
| 열네번째 이야기 - 이항분포 (0) | 2019.08.06 |
| 열세번째 이야기 - 모수,통계량,베르누이 시행,표본추출법 (0) | 2019.08.05 |