2019. 8. 1. 01:01ㆍ통계학이론/통계학개론
안녕하세요! 리그레션입니다 오늘은 상관계수에 대한 이야기를 가져왔습니다.
상관계수(Correlation Coefficient)는 자료를 그래프로 나타내었을 때 선형에 얼마나 가까운지를 나타내는 척도로 사용됩니다.
상관계수는 r로 표기를 하는데요,
조사된 n개의 자료쌍이 (X1,Y1),(X2,Y2), .... ,(Xn,Yn)일때 다음의 식을 생각해 볼까요?

여기서 xbar와 ybar는 각각 Xi와 Yi값들의 평균입니다. Sxy는 두 변수의 자료쌍 각각의 편차들의 곱을 합한형태를 하고 있는데요, 이는 다음의 성질을 가집니다.
첫째, Xi 값이 크면 Yi값도 크고, Xi 값이 작으면 Yi값도 작다면, Sxy값은 양의 값을 가지게 됩니다.
둘째, Xi 값이 크면 Yi값이 작고, Xi 값이 작고 Yi값이 크다면, Sxy값은 음의 값을 가지게 됩니다.
셋째, Xi 값이 클 때 Yi값은 크기도 하고 작은 값을 가지기도 하고, Xi 값이 작을 때 Yi값은 크기도 하고 작기도 하다면, 즉 Xi값의 크기와 Yi값의 크기 사이에 관계가 없다면, Sxy값은 0에 가까운 값을 가지게 됩니다. 더해지는 값들이 서로 상쇄되기 때문이죠.
때문에 Sxy는 두 변수의 척도의 단위와 값의 크기에 따라 값이 좌지우지되기 때문에 선형관계를 나타내는 표준화된 척도로는 부적합했습니다. Sxy 는 두 변수의 자료쌍 각각의 편차들의 제곱을 합한 형태를 지니고 있으므로, 다음의 값들의 제곱근의 곱으로 나누어주면 이런 문제가 해결됩니다.

위의 계산으로 얻어지는 표준화된 척도를 상관계수(r)이라고 합니다.

일반적으로 상관계수를 구할 때는 빠른 계산을 위하여 다음의 계산식을 사용합니다.
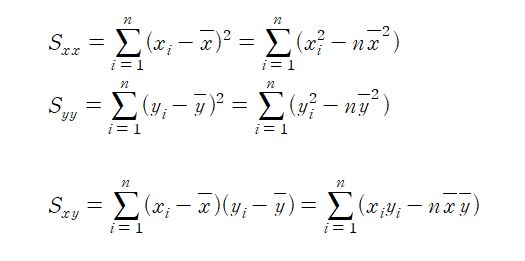
선형관계의 정도를 나타내는 상관계수는 다음의 성질을 가지는 데요,
1. r은 -1과 1사이의 값을 가집니다.

2. 그래프의 형태는 r>0이면 작은 쪽에서 큰 쪽으로 올라가는 형태를 취하고 1에 가까워질수록 기울기가 양인 직선에 가까워지고, ㄱ<0이면 큰 쪽에서 작은 쪽으로 내려가는 형태를 취하고 -1에 가까워질수록 기울기가 음인 직선으로 가까워지고, r이 0에 가까워질수록 원형으로 넓게 퍼지는 형태가 되어버립니다. 그리고 상관관계의 목적자체가 선형에 얼마나 가까운지를 나타내는 것이므로 반드시 산점도와 함께 사용되어야 합니다.
참고로 원인과 결과의 관계는 상관관계로 구할 수 없습니다. 예를 들어 매년 범죄율이 높아지는데 껌의 판매량이 같이 올라간다고 범죄율을 낮추기 위해 껌 판매를 제재하는게 옳을까요? 상관계수값이 1에 가깝다고 실제론 관계가 없을 수도 있습니다. 이것을 허위상관관계(spurious correlation)라고 합니다.
감사합니다 이상 상관관계에 대해 자세히 다루어 봤습니다. 모두 좋은 하루 보내세요~ 리그레션이었습니다.
'통계학이론 > 통계학개론' 카테고리의 다른 글
| 열한번째 이야기 - 확률변수와 기댓값 (0) | 2019.08.04 |
|---|---|
| 열번째 이야기 - 확률표본과 임의선택 (0) | 2019.08.02 |
| 여덟번째 이야기 - 사분위수와 이변량 자료 (0) | 2019.07.31 |
| 일곱번째 이야기 - 분산과 편차 (0) | 2019.07.30 |
| 여섯번째 이야기 - 평균과 중앙값 (0) | 2019.07.29 |